- c'est l'angle entre le méridien qui passe par un point et le nord de la projection ;
- cet angle peut atteindre plusieurs degrés (positif ou négatif).
fig. 6a - Convergence des méridiens
Sources : www.ign.fr
V.2.5 - Dernière mise à jour : 27/02/2023
- L'objectif prioritaire lors de la projection d'une sphère sur un plan
c'est de limiter les déformations
En fonction du but à atteindre,
on choisit de conserver localement :
- les angles => projection conforme
pour se localiser, se diriger
- les surfaces => projection équivalente
pour la cartographie à petite échelle
En fait, elle conserve le rapport entre les surfaces mesurées sur la terre et les surfaces mesurées sur la carte.
- ni l'un ni l'autre => projection aphylactique
Comme aucun système ne peut être à la fois conforme et équivalent, les projections aphylactiques sont des solutions de compromis qui compensent au mieux les diverses altérations (Sources : CERTU, RGF93_theorie_et_concept_CERTU.pdf.
- Une projection est dite "équidistante" lorsqu'elle conserve les distances à partir d'un point donné.
Mais, aucune projection ne peut conserver toutes les distances.
- Dans la plupart des projections, le Nord de la projection n'indique pas la direction du pôle Nord géographique.
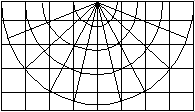
Mise en évidence de la convergence des méridiens :
- c'est l'angle entre le méridien qui passe par un point et le nord de la projection ;
- cet angle peut atteindre plusieurs degrés (positif ou négatif).
fig. 6a - Convergence des méridiens
Sources : www.ign.fr
fig. 6b - Convergence des méridiens
Sources : Arwann.com
fig. 6c - Les nords : quadrillage (projection) GPS en bleu et géographique sur une TOP25
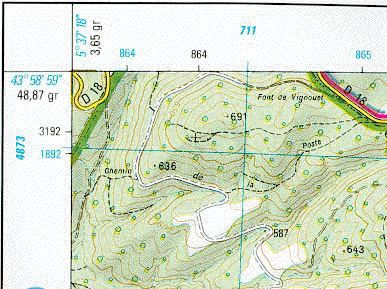
Sources : Carte Top25 3342 OT - Manosque Forcalquier, 1ère édition, 1996
- Dans la plupart des lieux, le pôle Nord magnétique n'est pas dans la direction du pôle Nord géographique.
L'angle entre le Nord magnétique et le Nord géographique s'appelle la déclinaison magnétique.
Pour plus d'information sur le pôle Nord magnétique cliquez ici
Pour plus d'information sur le champ magnétique terrestre cliquez ici
Ce sont des projections sur des surfaces développables*
A savoir, les projections :
- cylindriques*
- coniques*
La surface de projection est un cylindre tangent ou sécant au modèle de la Terre.
- Le plus souvent observée dans sa variété directe*, mais aussi transverse*, plus rarement oblique*.
fig. 7 - Représentation cylindrique directe
Sources : www.ign.frfig. 8 - Représentation cylindrique oblique
Sources : www.ign.fr
Exemple de projection cylindrique oblique :
Nom de la projection cartographique Oblique Mercator
Facteur d'échelle de la ligne centrale: 0.999500
Azimut de la ligne oblique:
- Angle azimutal: 18.900000
- Longitude du point de mesure azimutale: 46.437200
- Latitude de l'origine de la projection: -18.900000
Sources : les métadonnées d'ESRI pour un fichier centré sur la région d'Antananarivo à Madagascar.
fig. 9 - Représentation cylindrique transverse
Sources : IGN in sat-info
- Les projections cylindriques sont un perfectionnement des cartes plates.
Cartes plates : report direct sur le plan des distances et des directions.
Synonyme : projection sur le plan tangent
- c'est la carte des explorateurs et des géomètres
- elle reste valable sur de faibles surfaces.
Les cartes plates appartiennent à la même famille (celle des projections sur un plan) que les projections azimutales, (encore appelée projection perspective ou zénithale) où le plan est lui même tangent au modèle de la terre [Exemple : Stéréographie polaire (carte du ciel, cartes des régions polaires,...)].
- La projection de Mercator (directe) est la plus célèbre. Elle est connue depuis le XVIe siècle.
Elle est conforme, mais son échelle :
- bien que constante sur un parallèle ;
- varie d'un parallèle à l'autre.
fig. 10 - Mercator directe
Sources : JOLY 1976, p.64
Elle est surtout utilisée pour :
- les cartes marines et aéronautiques ;
- les atlas des régions intertropicales.
Elle est de plus en plus abandonnée pour la réalisation des planisphères, en raison des distorsions engendrées sur les hautes latitudes au profit, entre autre, de la projection de Mollweide (projection équivalente).
- La projection de Mercator transverse (ou projection de Gauss ou projection cylindrique conforme de Lambert) est connue depuis le XVIIIe siècle.
Ses caractéristiques sont :
- projection axée sur un méridien central (ici le 90 E) qui est une droite ;
- l'équateur est une droite perpendiculaire à ce méridien ;
- les autres méridiens et parallèles sont des courbes transcendantes (non algébriques), orthogonales entres elles.
fig. 11 - Projection de Mercator transverse
Sources : JOLY 1976, p.64
C'est le système UTM qui est utilisé :
- pour la cartographie à moyenne et grande échelle ;
- entre le 80e N et le 80e S.
Il existe aussi maintenant, depuis 2005, des cartes dites Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator ou WGS 84/Pseudo-Mercator....
Ce sont des variantes de la carte de Mercator qui sont devenues, de facto, des standards pour la cartographie sur le Web !
C'est Google Map qui a initié le mouvement et maintenant tout le monde s'y est mis : Mapbox, Bing Maps, OpenStreetMap, Mapquest, Esri...
Voilà pourquoi on parle de standard !
- Qu'est-ce que cela change ?
À peu près rien à petite échelle !
Mais à grande échelle, alors que la Mercator "classique" utilise des formules de projections adaptées à la forme ellipsoïdale de la Terre la Web-Mercator reste sur du sphérique !
Des déviations mineures à
petites échelles qui peuvent atteindre 40 km à grande échelle loin de
l'équateur
Méfiez-vous des calculs de
distances sur Google Map (et autres Pseudo-Mercator) ! (pour
aller plus loin) ou (un peu plus loin encore) (: !
La surface de projection est un cône tangent ou sécant au modèle de la Terre.
Elle est surtout utilisée :
- pour les cartes à grande échelle ;
- dans sa variété directe.
Elle existe sous deux forme :
fig. 12 - Représentation conique directe tangente
Sources : www.ign.frfig. 13 - Représentation conique directe sécante
Sources : IGN in sat-info
Exemple : Lambert, Lambert-93, Bonne, ...
En général,
- les méridiens sont concourants et rectilignes ;
- les parallèles sont en arcs de cercles concentriques ;
- On appelle lignes automécoïques les intersections entre l'ellipsoïde et le plan de projection
La zone encadrée par les parallèles de contacts (automécoïques) est un secteur où la déformation est minimale.
- Les projections coniques conformes de Lambert (XVIIIe siècle) :
- ont été introduites dans l'armée pour faciliter les tirs d'artillerie ;
- sont devenues la base de la cartographie française à grande échelle.
fig. 14 - Projection conique conforme de Lambert
Sources : JOLY 1976, p.67
- La projection de Bonne (XVIIIe siècle) est surtout connue en France pour son 1/80 000 :
- dit carte d'État-Major ;
- sa couverture géologique avant remplacement par le 1/50 000.
Ce n'est toutefois pas une vrai projection conique, les méridiens ne sont pas des droites concourantes.
fig. 15 - Canevas de Bonne
Sources : JOLY 1976, p.67Il y en a un très beau à découvrir en même temps que l'article sur les projections cartographiques de Wikipédia.
Pour approfondir ces aspects, se référer aux ouvrages en bibliographie et en bibliothèque de Jacques BERTIN (BERTIN 1973, pp. 287-295) ou de Fernand JOLY (JOLY 1976, pp.53-74), par exemple.
fig. 16 - Quelques exemples proposés par le support ESRI
Sources : ESRI
- Quel est le planisphère utilisé dans Google Map ? voir ICI
Voir les déformations engendrées en faisant le test LÀ
- Qui du
Groenland ou de l'inde est le plus grand pays (surface) ?
- Quelle est la projection utilisée ICI par l'Union européenne ?
- Comment faire pour
trouver la réponse ?
Toutes ces projections ont un code (presque) unique attribué par l'European Petroleum Survey Group (EPSG).
À l'origine, ce sont des pétroliers, dont le groupe ELF, qui se dotent d'une liste des systèmes de coordonnées géoéréférencées de projection. Ils ont été intégrés dans la plupart des logiciels SIG. Ce sont maintenant des standards de l'OGC (Open Geospatial Consortium).
- Saurez-vous, avec les éléments présents sur cette carte, retrouver sa projection ?
fig. 17 - NE-29-XXIV
Sources : IGN
Un site très complet sur les représentations, donc les projections : Wikiniversité
|
Communiquez-moi sur la plateforme Moodle, à la rubrique "Questions de cours", les réponses aux questions suivantes :
Question n°2.2.1. Les cartes marines doivent permettre le déplacement d'un point à un autre. Elles doivent donc être :
Question n°2.2.2. Sur quelle projection cylindrique les pôles sont rejetés à l'infini :
Question n°2.2.3. Une représentation conique qui a deux automécoïques est une représentation :
|
NB : les mots suivis de "*" font partie du vocabulaire géographique, donc leur définition doit être connue. Faites-vous un glossaire.