Présentation de l'aide à la décision multicritère
(Multi-Criteria Decision Analysis)

1. En guise d'introduction

• thèmes abordés ;
• dates des exemples traités ?

- Et en géo ?

1.2. Dans quelles applications ?

Des exemple pour les logiciels propriétaires de traitement des données :

XLSTAT utilise, entre autres comme méthodes :

• AHP

• Electre

Excel est utilisé par des développeurs mais on ne connaît pas la méthode a priori :

• 1001tableurs ;

• 2022 Modèles EXCEL ;
  

• Everlaab...

Mais ce n'est pas très spatiale...

2. Quelques principes de base du MCDA (rappel : Multi-Criteria Decision Analysis)

- Quand a-t-on recours à l'AMC ?

Probablement quand on n'a pas d'échantillons de terrain pour modéliser l'aptitude

Sinon, on procéderait par régression ou autre (à discuter !)

Sans paraphraser ce qui a très bien été énoncé par le Clark Labs dans son chapitre sur les MCE et qui est repris en français ici (mem01mas.htm), il convient d'insister sur les points suivants :

Décision = choix parmi plusieurs alternatives.

Critères (criteria) = éléments de base d'une décision. Peuvent être évalués ou mesurés. Il en existe 2 sortes :

- les facteurs = exprimés par une échelle de mesures continues (ex. plus la pente est faible, mieux c'est !) ;

- les contraintes = exprimés par une échelle de mesures discrètes (ex. apte sous 30°, inapte au-delà !)

Le facteur agit de façon progressive, la contrainte est un facteur limitant.

Le MCDA se subdivise en deux sous partie :

- l'analyse multicritère proprement dite (AMC ou MCE) => recherche d'un ou plusieurs sites aptes à l'installation d'un équipement (un seul objectif)

- l'analyse multiobjectif (AMO ou MODA) => recherche d'un ou plusieurs sites aptes à l'installation d'équipements antagonistes ou non comme la recherche de sites aptes à accueillir :

- une médiathèque ;

VS

- une salle multisport

Recherche d'un ou plusieurs sites aptes à l'installation d'équipements concurrents (Multi-Objective Land Allocation MOLA)

fig. 1 - Conflit d'objectifs

Sources : Eastman et al. 1995

3. Méthodes d'évaluation multicritère

3.0. Les étapes du MCE

3.1. Fixer l'objectif/définir le problème

En règle générale, un objectif doit être :

S => specific / spécifique

M => measurable / mesurable

A => attainable / réalisable

R => relevant / pertinent

T => time-bound / limité dans le temps

L'origine de l'acronyme remonterait à 1981, depuis ont été ajoutés Ethical et Recorded pour faire SMARTER (: !

3.2. Déterminer les critères (facteurs/contraintes)

- A-t-on besoin de tout le réseau viaire d'une ville ou seulement des artères principales => quelle base de données les contient ?

- Les critères doivent être mesurables

S'ils ne le sont pas, il faut utiliser des proxies [variables substituées en raison d'un comportement similaire = forte corrélation, comme les eaux libres, les zones humides et les cours d'eau (comme substituts pour les eaux souterraines)]

- Auriez-vous un exemple ?

3.3. Normaliser/Standardiser/Reclasser les scores des facteurs/critères

- Définir les valeurs d'aptitude des facteurs sur une échelle commune pour rendre les comparaisons possibles, comme par exemple, du moins apte au plus apte :

- 0 à 1 (échelle continue, décimale, utilisée dans ArcGIS Pro et TerrSet)

- 0 à 10 (échelle discrète utilisée dans ArcGIS Desktop)

- 0 à 100

- 0 à 255 (256 niveaux = un octet, ancienne échelle d'IDRISI)

- Pour comparer des valeurs de pentes (% ou °), d'altitudes (m ou feet) ou de distances (km ou statute mile / U.S. Survey mile) dont les unités diffèrent.

fig. 2 - Standardisation des valeurs prises par les facteurs (échelle 0 - 255)

Sources : Estoque 2011

- Le principe, le plus simple ici, repose sur un étalement de la dynamique entre deux bornes communes à l'ensemble des critères.

Sources : Eastman et al. 1995

où les paramètres de la fonction de transformation sont les suivants :

X_i = nouvelle valeur transformée ;

R_i = ancienne valeur dans l'unité d'origine ;

R_min = ancien minimum dans l'unité d'origine ;

R_max = ancien maximum dans l'unité d'origine ;

m = nouvelle étendue (1 ; 10 ; 100 ; 255...)

- Deux reclassifications différentes sont à envisager, selon que l'on traite une donnée :

- numérique (pentes, distances, profondeur, coûts...) ;

- catégorielle (occupation du sol, type de routes, zonage cadastral...).

Ces fonctions ont toutes plus ou moins le même nom, par exemple :

- Assign ou Reclass dans TerrSet ;

- Reclassify dans ArcGIS ou QGIS, etc.

3.3.1. Reclassification des valeurs catégorielles

tab. 1 - Exemple de reclassification sur les valeurs

VALUE	New values	Descriptions (for reference only)
1	1	Developed, High Intensity
2	1	Developed, Medium Intensity
3	2	Developed, Low Intensity
...	...	...

Sources : ESRI

3.3.2. Reclassification des valeurs numériques continues

- Par exemple, pour ArcGIS, il existe un descriptif de l'ensemble des méthodes de reclassement

Pour ArcGIS Pro => Vue d'ensemble du jeu d'outils Raster - Reclassement

Ce sont des classifications standards qui proposées dans ces pages d'ArcGIS Pro => Méthodes de classification des données

Comme la méthode dite des intervalles égaux utilisée dans le TP (mem21mas.htm)

- Dans le cas de ce TP (mem21mas.htm) diffusé entre 1995 et 2012 et destiné à prendre en main l'outil Spatial Analyst, la méthode de classification préconisé est la superposition pondérée (Weighted Overlay).

Elle consiste à convertir des jeux de données à virgule flottante, continus (distances en mètres, pentes en degrés ou en pourcentages...), en valeurs entières discrètes à affecter à des plages de valeurs (cf. Reclassification des jeux de données dans mem21mas.htm).

À titre d'exemple, si la limite d'aptitude est de 21%, est-ce qu'un terrain doté d'une pente à 20.9% est réellement plus apte qu'un terrain doté d'une pente à 21.1% ?

Les méthodes Weighted Overlay et Weighted Sum, par exemple, sont parfois qualifiées de rigides (crisp) car les limites sont trop strictes (sharp).

- Depuis les premières versions d'IDRISI, IDRISI32 au moins, une fonction relevant de la théorie des ensembles flous (fuzzy set theory) est disponible dans le module MCE.

La logique floue traite spécifiquement des situations où les frontières entre les classes ne sont pas claires (nettes/sharp).

La logique floue est basée sur la théorie des ensembles.

En 1965, Lotfi Aliasker Zadeh présente sa théorie des ensembles flous et la logique floue.

En 1978, il en crée une extension, la théorie des possibilités (in Que-sais-je ? : Théorie des possibilités), c'est une alternative à la théorie des probabilité pour représenter l'incertitude (in Wikipedia : Théorie des possibilités).

Par conséquent, vous définissez des possibilités, pas des probabilités quand vous faites de la "fuzzyfication" (!) en MCDA !

L'appartenance à la classe va osciller entre :

0 => la valeur ne fait pas partie de la classe ;

1 => la valeur fait partie de la classe.

Toutes les autres valeurs correspondent à un certain niveau de possibilité, les valeurs les plus élevées indiquant une plus grande possibilité d'appartenance.

fig. 3 - Premier exemple d'appartenance floue à une classe

Sources : ESRI 2014 - Applying fuzzy logic to overlay rasters

- Comment lire la figure n°3 ?

L'appartenance complète à chaque classe est la suivante :

•     Petit : < 5 pieds (1,524 mètres)
•     Moyen : de 5' 3 1/2" (1,6129 mètre) à 5' 8 1/2" (1,7399 mètre)
•     Grand : > 6' (1,8288 mètres)

Mais qu'en est-il des tailles comprises entre :

- 5 pieds (1,524 mètres) et 5' 1 3/4" (1,6193 mètres) => elles sont plus susceptibles d'être dans l'ensemble des petits ;

- 5' 1 3/4" (1,6193 mètre) et  5' 3 1/2" (1,6129 mètre) => elles sont possiblement dans l'ensemble des petits mais ont une plus grande possibilité de faire partie de l'ensemble moyen, etc.

- Le processus de fuzzification caractérise l'imprécision des classes pour les phénomènes qui n'ont pas de frontières bien définies.

fig. 4 - Deuxième exemple d'appartenance floue à une classe

Sources : ESRI 2014 - Applying fuzzy logic to overlay rasters

- Comment lire la figure n°4 ? Comment appartenir à un groupe aux frontières floues ?

- Une valeur répondant exactement aux critères se voit attribuer la valeur 1 ;

- Celles qui sont complètement hors des critères se voient attribuer la valeur 0 ;

- Au fur et à mesure que les valeurs s'éloignent de l'idéal (centre de l'ensemble), on leur attribue une valeur décroissante sur une échelle continue de 1 à 0 (À mesure que les valeurs attribuées diminuent, la valeur du phénomène d'origine a moins de possibilité d'être membre de cet ensemble) ;

- La valeur de fuzzification de 0,5 est le point de croisement / bascule.

- De façon plus pragmatique, le graphique de la figure n°5 permet de comprendre la différence entre seuil flou (fuzzy) et un seuil strict ou net (crisp).

fig. 5 - Fonctions d'appartenance à un ensemble flou ou net

Sources : Eastman 2009 in IDRISI Taiga

- Les fonctions de fuzzification, comme ici dans IDRISI (cf. fig. 6abc), permettent d'adapter la classification aux phénomènes étudiés.

fig. 6abc - Choix des fonctions d'appartenance floue dans IDRISI

Sources : Eastman 2009 in IDRISI Taiga

- Si l'on reprend les exemples développés dans le tutoriel de prise en main de TerrSet 2020, la dernière version d'IDRISI, au chapitre 2.8 "MCE: Non-Boolean Standardization and Weighted Linear Combination" plusieurs standardisations sont proposées avec différentes fonctions de standardisation :

• pour standardiser la distance entre un futur lotissement et le centre ville, c'est la fonction linéaire monotone décroissante qui est préconisée (cf. fig. 6b Linear Membership Function, graph. L2)
• plus on s'éloigne, quelque soit la distance, plus l'aptitude diminue ;
• il n'y a pas d'effet seuil ;
• les bornes retenues sont :
• c => 0, le minimum ;
• d => le maximum lu sur la carte (582, c'est un coût, issu d'un calcul de distance-coût)

• pour standardiser la distance entre un futur lotissement et les plans d'eau et autres rivières, c'est la fonction sigmoïde monotone croissante qui est préconisée (cf. fig. 6a Sigmoidal Membership Function, graph. S1)
• plus on s'éloigne, quelque soit la distance, plus l'aptitude augment ;
• il n'y a des effets de seuil :
• pas de construction possible à moins de 50 m (l'aptitude prend la valeur 0) ;
• l'aptitude commence de croître entre 50 et 100 m (a = 100 m) ;
• elle croit entre 100 et 800 m (b = 800 m, distance à laquelle l'aptitude commence à se stabiliser et approche de 1) ;
• elle est à peu près équivalente, à dire d'expert, entre 800 et 1 000 m (l'aptitude prend la valeur 1 et reste à 1au-delà)

Dernier exemple,

• pour standardiser la distance entre un futur lotissement et la route d'accès, c'est la fonction en forme de J (J-shaped) monotone décroissante qui est préconisée (cf. fig. 6c J-shaped Membership Function, graph. J2)
• au-delà de 50 m de la route, plus on s'éloigne, plus l'aptitude diminue ;
• mais elle reste acceptable jusqu'à 400 m ;
• les bornes retenues sont :
• c => 50, avant 50 m aptitude maximale ;
• d => 400 m, au-delà c'est encore très faiblement apte et comme c'est asymptotique, cela n'atteindra jamais 0 !

- Auriez-vous quelques exemples à décortiquer ?

Si cette approche par fuzzification est ancienne dans IDRISI, il faut attendre le milieu des années 2010 pour qu'elle intègre les exemples de prise en main du module Spatial Analyst d'ESRI.

- Les nouvelles versions pour :

- ArcGIS Desktop => Suitability modeling workflow using ArcGIS Desktop—Lesson 2: Transforming data onto a common scale

- ArcGIS Pro => Suitability modeling workflow using ArcGIS Pro—Lesson 2: Transforming data onto a common scale

ont adopté une approche plus souple relevant de la logique floue (fuzzy).

3.4. Déterminer le poids de chaque facteur

3.4.1. Revue des méthodes

Estoque (Estoque 2011) évoque plusieurs méthodes, dont certaines mériteraient que l'on recherche si elles sont encore en en usage ! Il s'agit du Ranking et du Rating.

Il les décrit comme suit :

• Ranking (classement)
• s'il y a 3 facteurs, il faut les classer comme suit : facteurs 1, 2 et 3, où 1 est le moins important
  alors que 3 est le plus important.
• Rating (évaluation/notation)
• s'il y a 3 facteurs, il faut les noter à l'aide du centile : facteur 1 avec le pourcentage le moins important et facteur 3 avec le pourcentage le plus élevé car le plus important.

Car la méthode la plus répandue relève de la comparaison par paire.

Développée par Thomas L. Saaty et publié en 1977 (Saaty 1977) dans le cadre d'une étude de processus de prises de décision connu sous le nom de processus de hiérarchie analytique (AHP).

• Comparaison par paire => Analytical Hierarchy Process (AHP)
  
• Une matrice 2 x 2 est construite, chaque critère y est comparé aux autres, l'un après l'autre, et, en fonction de qui est le plus important il reçoit une note, sur une échelle allant de 1 à 9. Où :
• 1 = préférence égale entre deux facteurs ;
• 9 = un facteur particulier est extrêmement important par rapport à l'autre.
• une estimation des pondérations est calculée et utilisée pour dériver un rapport de cohérence (CR, consistency ratio) des comparaisons par paire.
• Si le CR > 0,10, il faut revoir certaines notations ; le processus est répété jusqu'à ce que la valeur souhaitée de CR soit atteinte (CR < 0,10).
• Donc, comme dans le Ranking et le Rating, les pondérations dans l'AHP sont également exprimés en valeurs numériques dont la somme vaut 1.

3.4.2. L'Analytical Hierarchy Process (AHP) en pratique

En 4 étapes !

1. Comparaison des facteurs par paire
2. Complétion de la matrice de comparaisons
3. Normalisation et détermination des pondérations
4. Calcul de la cohérence des pondérations

Pour ne pas alourdir cette fiche mémo, le développement pratique de l'AHP est renvoyé dans la fiche mémo mem13ma1.htm

3.5. Agréger les critères

L'évaluation multicritères (MCE) est le plus souvent obtenue à l'issue d'une des procédures suivantes, seule ou combinée à une autre :

• Superposition booléenne => Boolean overlay
• Combinaison linéaire pondérée => Weighted Linear Combination (WLC)
• Ordered Weighted Average (OWA)

3.5.1. Superposition booléenne

C'est la superposition par contraintes : c'est oui ou c'est non ! Possible ou impossible (construire en zone inondable...)

Tous les critères, les couches rasters le plus souvent, sont réduits à des déclarations logiques d'adéquation ou d'aptitude (codées en 0 ou 1 => logique booléenne),

puis combinés au moyen d'un ou plusieurs opérateurs tels que l'intersection (AND) et l'union (OR)

fig. 7 - Superpositions de cartes et logique booléenne

Sources : David Harbor, Washington and Lee University

Selon l'opérateur booléen utilisé, les prises de décision sont antagonistes !

Comparons la combinaison des critères avec les opérateurs logiques AND (opérateur d'intersection) et OR (opérateur d'union)

- ET logique, un emplacement doit répondre positivement à tous les critères pour être inclus dans l'ensemble de décision :

- Si un seul critère n'est pas rempli, l'emplacement est exclu ;

- Il faut que toutes les couches valident le test (cf. A and B, fig. 7) ;

- Une telle procédure est dite "averse" au risque.

C'est la stratégie de la prudence.

- OU logique, un emplacement est inclus dans l'ensemble de décision :

- Si seulement un seul de ses critères réussit le test (cf. A or B, fig. 7) ;

- Il s'agit donc d'une stratégie avec une prise de risque importante.

3.5.2. Combinaison linéaire pondérée (WLC)

Ici, les critères continus (facteurs) sont standardisés sur une plage numérique commune, puis combinés au moyen d'une moyenne pondérée.

La carte d'aptitude croissante qui en résulte peut ensuite être masquée par une ou plusieurs contraintes booléennes pour tenir compte des exclusions localisées.

Ensuite, si nécessaire, un seuillage est effectué pour identifier les zones les plus aptes.

fig. 8 - Position théorique d'une aptitude WLC entre le AND et le OR (d'après le Clark Lab)

Sources : TerrSet Tutoriel2020

La position du point MCEWLC, issu d'un exercice de TerrSet (cf. 2-9 TerrSet Tutoriel2020), caractérise une position intermédiaire entre le comportement "risque averse" du AND et le comportement "risque tout" du OU.

La compensation est totale (full tradeoff) avec la procédure WLC.

Il est possible de faire varier cette compensation (entre les positions pas de compensation et compensation intégrale, no tradeoff et full tradeoff) avec la procédure OWA, une autre spécialité d'IDRISI.

Dans le cas du WLC, les critères sont combinés en appliquant un poids à chacun suivi d'une sommation des résultats pour produire la couche d'aptitude, comme suit :

Sources : Eastman et al. 1995

où :

S = aptitude (suitability) ;

W_i = le poids du facteur i (weight) ;

X_i = la valeur du critère i.

Si des contraintes booléennes s'appliquent également, la procédure est modifiée en multipliant l'aptitude précédente par le produit des contraintes, comme suit :

Sources : Eastman et al. 1995

S = aptitude (suitability) ;

W_i = le poids du facteur i (weight) ;

Xi = la valeur du critère i ;

C_j = valeur de la contrainte j ;

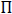π = produit des contraintes (1 apte, 0 inapte)

Dans le cadre de la procédure d'évaluation multicritère MCE, utilisant la combinaison linéaire pondérée (WLC) décrite ci-dessus, il est nécessaire que la somme des pondérations soit égale à un.

3.5.3. Moyenne pondérée ordonnée (OWA)

Au-delà de la combinaison linéaire pondérée (WLC), la moyenne pondérée ordonnée (OWA) permet de contrôler la quantité de risques et de compromis que l'on souhaite inclure dans le résultat.

(fiche en travaux)

3.6. Valider/vérifier le résultat

Comment évaluer le résultat (qui est une modélisation et pas la réalité !) :

• Vérification de terrain
• Par échantillonnage de parcelles tests ;
• Analyse de l'instabilité : le résultat est-il robuste (sensibilité du résultat aux modifications du paramétrage) ?
• Comment les éléments suivants affectent-ils le résultat ?
• par modification "légère" de l'ensemble des critères (en plus ou en moins) ;
• par modification "légère" du poids respectifs des facteurs ;
• Le résultat est-il correct/cohérent ?
• Le résultat reflète-t-il la réalité ?
• ...

4. Test de compréhension