Parmi les méthodes les plus courantes (pour rappel de la fiche mémo mem12mas.htm) :
- Processus de hiérarchie analytique - AHP (Analytical Hierarchy Process) ;
- Combinaison linéaire pondérée - WLC (Weighted Linear Combination) ;
- Moyenne pondérée ordonnée - OWA (Ordered Weighted Averaging) ;
- Modèle de somme pondérée - WSM (Weighted Sum Model) ;
- Technique d'ordre de préférence par similarité avec la solution idéale - TOPSIS Model (Technique for order of preference by similarity to Ideal Solution) ;
- Élimination et choix exprimant la réalité - ELECTRE (Elimination and choice expressing reality) ;
- Programmation des objectifs - Goal Programming ;
- Modèle de produit pondéré - Weighted Product Model...
2. L'Analytical Hierarchy Process (AHP) en pratique
Comme présenté dans la fiche mémo mem12mas.htm), l'AHP se développe en 4 étapes :
- Comparaison des facteurs par paire
- Complétion de la matrice de comparaison
- Normalisation et détermination des pondérations
- Calcul de la cohérence des pondérations
À titre d'exemple, c'est un exercice de TerrSet (cf. 2-8 TerrSet liberaGIS 2025) qui est utilisé ici pour comparer les facteurs, remplir la matrice et faire la suite de la démonstration.
L'objectif est de sélectionner des zones aptes à recevoir un programme immobilier en fonction des couches d'informations suivantes :
- LANDUSE : occupation du sol autour de Westborough (MA, USA) ;
- TOWNDIST : distance-coût permettant de calculer le temps de trajet depuis le centre-ville jusqu'au bord de la couche ;
- WATERDIST : distance euclidienne aux eaux libres, les zones humides et les cours d'eau (comme substituts pour les eaux souterraines) ;
- ROADDIST : distance euclidienne aux réseaux routiers ;
- SLOPE : pente en p. 100 ;
- DEVELOPDIST : distance euclidienne aux zones déjà urbanisées.
2.1. Comparaison des facteurs
- Cette comparaison se fait avec l'échelle de Saaty (cf. fig. 1) reprise dans la littérature sous différente déclinaison, ici dans TerrSet Tutoriel2020.
fig. 1 - Échelle de comparaison des facteurs par paire
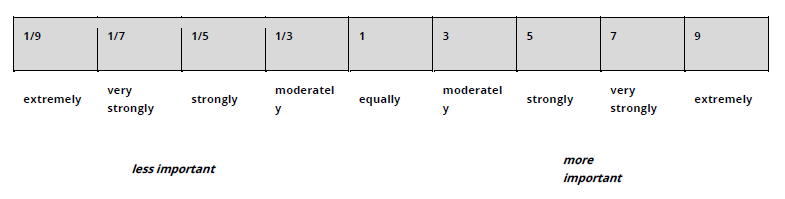
Sources : TerrSet liberaGIS 2025, Exercise 2-12, p.149.
Il est possible d'utiliser les valeurs paires (1/8 ; 1/6 ... 4 ; 6 ; 8) quand on hésite entre deux positions !
- Il convient de comparer des couches entre elles deux à deux en déterminant quelle est celle qui est la plus importante par rapport à l'autre.
- Est-ce que dans le choix d'un terrain à lotir (un groupement de pixels dans notre cas), la pente (SLOPE) est plus importante que la distance aux routes (ROADDIST) ?
On donnera les valeurs suivantes, par exemple, en fonction de la réponse :
- 1 => c'est équivalent ;
- 3 => modérément plus important ;
- 1/7 => très fortement moins important ;
- etc.
On conviendra que la part d'arbitraire peut être élevée !
- C'est pour cela que cette phase est l'objet de concertations entre experts ou d'enquêtes auprès des personnes concernées comme évoqué dans la littérature (exemple de la localisation d'une école à Surabaya en Indonésie, Haryprasetyo2016).
- Cette approche empirique est la justification de la méthode pour échapper à l'arbitraire.
- Plus le nombre de questionnaires sera élevé, plus fiable sera l'évaluation de l'importance des facteurs les uns par rapport aux autres.
- Des coefficients issus d'une régression pourraient sans doute jouer le même rôle.
- Ces couches ont été préalablement "fuzzifiées", c'est à dire traitées par une procédure de standardisation avec la procédure dite "FUZZY" dans TerrSet.
Ce sont elles que l'on retrouve dans la matrice des comparaisons présentée en figure n°2 avec l'extension "fuzz", une fois qu'elles ont été exprimées dans des valeurs comprises entre 0 et 1.
- LANDUSE => LANDFUZZ [occupation du sol autour de Westborough (MA, USA), où les valeurs : 1 ont été attribuées aux terres forestières ; 0,75 aux terres ouvertes non développées ; 0,5 aux zones sous pâturage ; 0,3 aux terres cultivées et 0 à toutes les autres catégories, de la plus apte à la moins apte] ;
- TOWNDIST => TOWNFUZZ [distance-coût permettant de calculer le temps de trajet depuis le centre-ville jusqu'au bord de la couche, où la valeur 1 touche la ville et 0 est au bord extrême de la couche] ;
- WATERDIST => WATERFUZZ [distance euclidienne aux eaux libres, les zones humides et les cours d'eau (comme substituts pour les eaux souterraines), où la valeur 0 est à 50 m de l'eau et tend vers 1 quand on atteint 1 000 m] ;
- ROADDIST => ROADDIST [distance euclidienne aux réseaux routiers, où la valeur 1 est à 50 m de la route et tend vers 0 en fonction de l'éloignement jusqu'à 400 m qui prend la valeur d'aptitude 0] ;
- SLOPE => SLOPEFUZZ [pente en p.100, où la valeur 1 est pour les pentes à 0 p.100 et tend vers 0 en fonction de l'augmentation de celle-ci jusqu'à 15 p.100 où elle prend la valeur d'aptitude 0] ;
- DEVELOPDIST => DEVELOPFUZZ [distance euclidienne aux zones déjà urbanisées, où 1 touche les zones déjà urbanisées et 0 est 1 325 m, distance maximale rencontrée] ;.
2.2. Complétion de la matrice des comparaisons
- Les facteurs, comparés deux à deux, sont ensuite stockés dans un tableau à double entrée.
Dans la procédure de pondération, WEIGHT pour TerrSet, seule
une demie matrice remplie est présentée (cf. figure n°2)
fig. 2 - La matrice des comparaisons (module WEIGHT - AHP dans IDRISI)
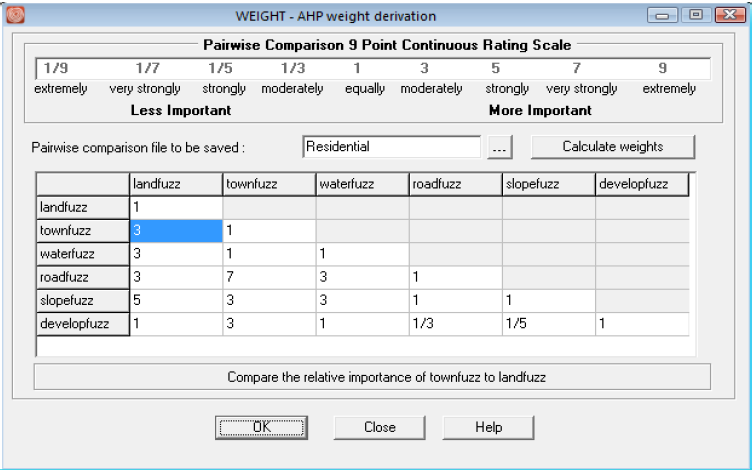
Sources : TerrSet liberaGIS 2025, Exercise 2-8, p.119.
Sens de lecture (horizontale par rapport à verticale), où on compare l'importance relative de :
- townfuzz par rapport à landfuzz (surligné en bleu) => 3 fois plus important !
- si c'était developfuzz par rapport à slopefuzz => 5 fois moins important !
Pour effectuer les traitements dans une feuille de calculs, les deux parties de la matrice sont complétées (symétrisées) comme dans le tableau n°1.
On retrouvera tous ces tableaux dans la feuille de calculs : m1fm13ta6.xlsx
tab. 1 - Complétion de la matrice
| LANDFUZZ | TOWNFUZZ | WATERFUZZ | ROADFUZZ | SLOPEFUZZ | DEVELOPFUZZ | |
| LANDFUZZ | 1.00 | 0.33 | 0.33 | 0.33 | 0.20 | 1.00 |
| TOWNFUZZ | 3.00 | 1.00 | 1.00 | 0.14 | 0.33 | 0.33 |
| WATERFUZZ | 3.00 | 1.00 | 1.00 | 0.33 | 0.33 | 1.00 |
| ROADFUZZ | 3.00 | 7.00 | 3.00 | 1.00 | 1.00 | 0.33 |
| SLOPEFUZZ | 5.00 | 3.00 | 3.00 | 1.00 | 1.00 | 0.20 |
| DEVELOPFUZZ | 1.00 | 3.00 | 1.00 | 0.33 | 0.20 | 1.00 |
| Somme colonne | 16.00 | 15.33 | 9.33 | 3.14 | 3.07 | 3.87 |
Une fois complétée, cette matrice doit être normalisée.
2.3 Normalisation et détermination des pondérations
La normalisation, ou standardisation, consiste à diviser chaque cellule par la somme de sa colonne (en dernière ligne du tableau n°1). On obtient ainsi des poids relatifs par cellule (cf. tableau n°2).
tab. 2 - Standardisation des cellules de la matrice
| LANDFUZZ | TOWNFUZZ | WATERFUZZ | ROADFUZZ | SLOPEFUZZ | DEVELOPFUZZ | |
| LANDFUZZ | 0.06 | 0.02 | 0.04 | 0.11 | 0.07 | 0.26 |
| TOWNFUZZ | 0.19 | 0.07 | 0.11 | 0.05 | 0.11 | 0.09 |
| WATERFUZZ | 0.19 | 0.07 | 0.11 | 0.11 | 0.11 | 0.26 |
| ROADFUZZ | 0.19 | 0.46 | 0.32 | 0.32 | 0.33 | 0.09 |
| SLOPEFUZZ | 0.31 | 0.20 | 0.32 | 0.32 | 0.33 | 0.05 |
| DEVELOPFUZZ | 0.06 | 0.20 | 0.11 | 0.11 | 0.07 | 0.26 |
Sources : TerrSet liberaGIS 2025
La moyenne des poids relatifs en ligne (W=Weight) va donner la valeur de la pondération pour chaque facteur (cf. tableau n°3).
tab. 3 - Pondération des facteurs
| LANDFUZZ | TOWNFUZZ | WATERFUZZ | ROADFUZZ | SLOPEFUZZ | DEVELOPFUZZ | W = Weight | |
| LANDFUZZ | 0.06 | 0.02 | 0.04 | 0.11 | 0.07 | 0.26 | 0.092 |
| TOWNFUZZ | 0.19 | 0.07 | 0.11 | 0.05 | 0.11 | 0.09 | 0.100 |
| WATERFUZZ | 0.19 | 0.07 | 0.11 | 0.11 | 0.11 | 0.26 | 0.139 |
| ROADFUZZ | 0.19 | 0.46 | 0.32 | 0.32 | 0.33 | 0.09 | 0.283 |
| SLOPEFUZZ | 0.31 | 0.20 | 0.32 | 0.32 | 0.33 | 0.05 | 0.254 |
| DEVELOPFUZZ | 0.06 | 0.20 | 0.11 | 0.11 | 0.07 | 0.26 | 0.133 |
| Somme des pondérations => | 1.000 |
Sources : TerrSet liberaGIS 2025
Ces valeurs de pondération par facteur (W) vont devenir les coefficients de pondération des méthodes d'agrégation : Combinaison linéaire pondérée (WLC) ou Moyenne pondérée ordonnée (OWA), si le ratio de cohérence/consistance (Consistency Ratio, CR) est validé à l'étape suivante.
La somme des coefficients de pondération doit être égale à 1 (cf. tab. 3).
2.4 Calcul de la cohérence des pondérations
Ces pondérations de facteurs (W) sont ensuite multipliées par leur pondération brute [c-à-d la somme de la colonne qui leur correspond (cf. tableau n°1), cf. col. W*Somme du tab. n°4].
| LANDFUZZ | TOWNFUZZ | WATERFUZZ | ROADFUZZ | SLOPEFUZZ | DEVELOPFUZZ | W = Weight | W*Somme | ||
| LANDFUZZ | 0.06 | 0.02 | 0.04 | 0.11 | 0.07 | 0.26 | 0.092 | 1.466 | |
| TOWNFUZZ | 0.19 | 0.07 | 0.11 | 0.05 | 0.11 | 0.09 | 0.100 | 1.534 | |
| WATERFUZZ | 0.19 | 0.07 | 0.11 | 0.11 | 0.11 | 0.26 | 0.139 | 1.296 | |
| ROADFUZZ | 0.19 | 0.46 | 0.32 | 0.32 | 0.33 | 0.09 | 0.283 | 0.888 | |
| SLOPEFUZZ | 0.31 | 0.20 | 0.32 | 0.32 | 0.33 | 0.05 | 0.254 | 0.780 | |
| DEVELOPFUZZ | 0.06 | 0.20 | 0.11 | 0.11 | 0.07 | 0.26 | 0.133 | 0.512 | |
| Somme des pondérations => | 1.000 | 6.477 | <= 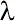 max
max |
Sources : TerrSet liberaGIS 2025
- Pour accéder au résultat de l'indice de cohérence (CI, Consistency Index), qui va nous permettre de savoir si nos pondérations sont rationnelles et cohérentes (consistency),
il faut effectuer la somme de la
colonne W*Somme, celle-ci se nomme la valeur propre (eigenvalue)
et s'écrit 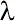 max.
(SAATY, 1980)
max.
(SAATY, 1980)
- Une fois calculée, nous allons successivement calculer l'indice de cohérence (CI) puis le ratio de cohérence (CR, Consistency Ratio).
CI = (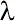 max - n) / (n - 1)
max - n) / (n - 1)
où n est le nombre de facteurs
CI = (6.477 - 6) / (6 - 1) = 0.095
- Pour savoir si notre indice de cohérence est rationnel, relève de pondérations équilibrées, il faut le diviser par un indice de cohérence aléatoire, il devient alors le ratio de cohérence (CR).
- Si CR > 0.10 (ou 10%) alors l'indice est incohérent (inconsistency, SAATY, 1980), il faut revoir les pondérations !
- Si CR < 0.10 l'indice est cohérent et on peut utiliser les pondérations (W=Weight) dans les méthodes d'agrégations comme WLC ou OWA par exemple !
- Le ratio de cohérence (CR) est calculé comme suit :
CR = CI / RI
tab. 5 - Indice de cohérence aléatoire (RI, Random Consistency Index)
| n | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.41 | 1.45 | 1.49 |
Sources : SAATY, 1980
- Dans notre exemple
Pour n = 6 facteurs
CR = 0.095 / 1.24 = 0.077
CR < CI car 0.077 < 1.24 donc CI est
cohérent, les pondérations des facteurs sont exploitables !