Vincent GODARD
Département de Géographie
Université de Paris 8
V.1.7.2 - Dernière mise à jour : 08/12/2017
Fiche Mémo n°1.1. du cours de SIG et analyse spatiale :
Géographie et analyse spatiale
Après avoir posé, de façon quasi axiomatique, l'approche scientifique d'une certaine forme de géographie (mem42enq.htm), il convient de s'intéresser à cette science sociale au travers de son ancrage dans l'espace.
Mais avant d'aborder les relations entre objets ponctuels, linéaires ou zonaux, le concept de distance et quelques autres questions métaphysiques seront abordées ici.
D'abord, existe-t-il des lois de (et dans) l'espace ?
Pendant la durée des travaux (et même après), on consultera avec intérêt le site de Claude Grasland consacré à ces aspects, en particulier le chapitre sur les distances, et le chapitre 1 de l'ouvrage d'analyse spatiale de Denise Pumain et Thérèse Saint-Julien
Pour les étudiants ne se souvenant plus de la différence entre les modes raster et vecteur, un petit coup d'oeil sur le fiche mémo mem11car.htm est indispensable.
1. Du point central à la dispersion, un arrière goût de statistique
Comme on le verra dans le chapitre sur les formes de la Terre (mem21sig.htm), il existe plusieurs "types" de coordonnées pour positionner un objet à la surface de celle-ci.
Elles sont en général appelées : X ; Y ; Z
Dans le cas des coordonnées géographiques :
- X est remplacée par la lettre grecque
(lambda) qui désigne la longitude ;
- Y est remplacée par la lettre grecque
(phi) qui désigne la latitude ;
- Z est remplacée par la lettre h qui correspond à la hauteur ellipsoïdale (qui diffère, au moins en théorie avec l'altitude, pour ne pas les confondre, voir la section 1.4 de la fiche mémo mem21sig.htm) ;
On pourrait même rajouter T, le temps, et avoir non plus un triplet (X;Y;Z) mais un quadruplet (X;Y;Z;T)
Ces coordonnées caractérisent un point à la surface de la Terre.
par définition, un point n'a pas de surface !
Exemple :
- Quelles sont les coordonnées de la Fac sur Google Earth ?
- En tous points de la fac ?
- Quelle est la différence entre la "notion" de lieu et le "concept" de points ?
On peut donc attribuer une valeur à un lieu (une fois que l'on a précisé sa définition !) :
- un nom (Université de Paris 8) ;
- une quantité (nombre d'étudiants en 2050 !) ;
Mais un lieu reste une abstraction dont l'implantation (voir fiche mémo 1.2 du cours de carto sur les variables visuelles) peut être :
- ponctuelle ;
- linéaire ;
- zonale (surfacique).
Par soucis de simplification, dans les sections suivantes, on ne retiendra que le couple de coordonnées (X;Y) et le raisonnement sur les distances se fera sur un semis de points. Les distributions de lignes et de zones seront abordées plus loin.
1.1 Les coordonnées, un avant goût de distance
Quand on se pose la traditionnelle question :
- Pourquoi là et pas ailleurs ?
Deux écoles s'affrontent !
À l'origine d'une situation, il est souvent évoqué le prima du lieu sur les relations, puis des relations sur les lieux.
- les lieux => situation absolue
caractères souvent liés à la topographie et aux conditions naturelles : cols, gués, anses
- les relations => situation relative
caractères souvent aux contacts (complémentarités, concurrences...) : à mi distance de..., sur la route de...
Mais en fait les deux se combinent assez rapidement !
Exemple :
- Pourquoi y a-t-il des tiques dans ce site ?
Quelques explications liées aux situations absolues et relatives :
- présence de conditions écologiques particulières...
- lieu de passage, de rassemblement de mammifères (hommes, grandes faunes, micromam'), d'oiseaux...
Pour des questions de simplicités d'utilisation, on préfère les :
- coordonnées rectangulaires planes (planaires)
aux
- coordonnées géographiques angulaires.
Pour tout savoir sur les coordonnées, cliquez ici !
C'est le cas des coordonnées en projection comme celle des grilles Lambert ou UTM qui sont comptées positivement vers l'est et le nord.
1.2 Approche vertical ou horizontale
La distance à quelque chose
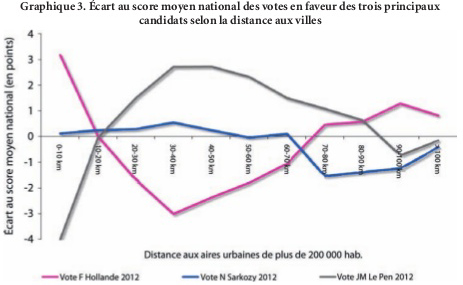
fig. 3 - Exemple classique du comportement électoral et distance au centre
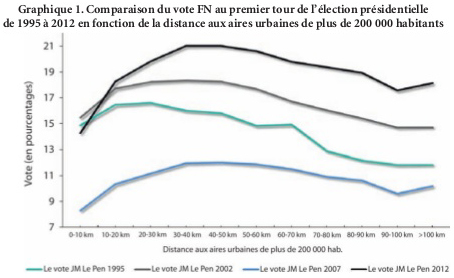
fig. 4 - Exemple classique du comportement électoral et distance au centre

2. Des coordonnées aux distances
2.1 Les coordonnées planaires ou en projection
Les coordonnées planaires sont les plus simples à utiliser,
mais sont moins précises que les coordonnées angulaires.
Cependant, leur altération, par rapport aux coordonnées angulaires, reste acceptable si on les utilise sur de petites portions de la surface terrestre.
fig. 1 - Des points et leurs coordonnées dans un repère orthonormé (type Lambert2e, Lambert93, UTM31n...)
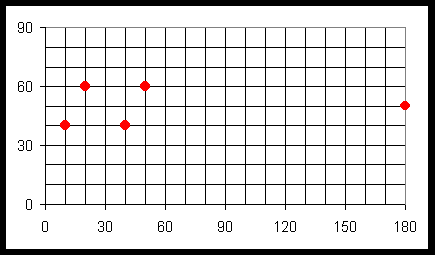
Sources : Cours de Claude Grasland, 2000-2001
Donc, à petite, voire à très petite échelle, on utilisera les coordonnées angulaires pour effectuer des calculs de distance, surfaces...
2.2 Des coordonnées planaires à la matrice des distances
- La position absolue est données par les coordonnées relevées sur la figure 1
et stockées dans le tableau 1
tab. 1 - Coordonnées planaires des points de la figure 1
i Xi Yi 1 20 60 2 50 60 3 10 40 4 40 40 5 180 50
- La position relative donne accès à la distance.
La distance est une mesure de l'écart spatial entre deux lieux.
Son calcul nécessite de transformer le tableau des coordonnées en matrice de distances.
La distance possède un statut explicatif dans la plupart des théories de la géographie actuelle.
En l'absence de contraintes d'itinéraires (linéaires ou autre comme les réseaux de routes, couloirs aériens...),
la position relative des lieux est couramment calculée à "vol d'oiseau".
Cependant, il existe d'autres façons d'aller de i à j (voir figure 2).
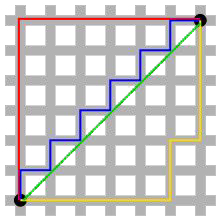
fig. 2 - Distance euclidienne et distance rectilinéaire
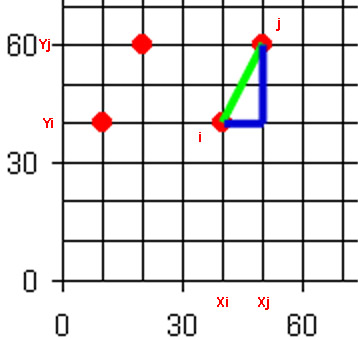
Sources : d'après Claude Grasland, 2000-2001
Pour calculer la distance qui sépare i de j, il existe plusieurs métriques.
La plus connue, celle du "vol d'oiseau", est dite :
- euclidienne, en vert sur le figure 2.
Celle, dite de Manhattan, ou rectilinéaire, en bleu sur le figure 2, est moins connue.
Les métriques sont des distances abstraites. En mathématique, elles vérifient quatre propriétés :
- pas de distances négatives : Dij > ou = 0 ;
- si Dij = 0, alors i = j ;
- les distances sont symétriques : Dij = Dji ;
- inégalité triangulaire avec : Dik < Dij + Djk
en géographie, parfois moins ;-)
Il existe plein de métriques différentes. On choisi la plus adaptée à sa problématique.
En général, celle des SIG (à grande échelle), est la métrique euclidienne.
2.3 La distance euclidienne (à vol d'oiseau)
- La distance euclidienne est calculée dans le plan.
formule n°1 - (mem11sig.htm)
La plus courante dans les SIG.
Mais,
- Suppose que l'on puisse se déplacer comme un oiseau ou un patineur => dans toutes les directions
- pas de directions ni d'itinéraires privilégiés
- pas d'obstacles
Sous estimerait les distances routières de 15 à 30 p.100 pour le réseau routier français.
tab. 2 - Distances euclidiennes entre les points de la figure 1
DEij 1 2 3 4 5 1 0 30 22 28 160 2 30 0 ? ? ? 3 22 ? 0 ? ? 4 28 ? ? 0 ? 5 160 ? ? ? 0 Il faut compléter le tableau en téléchargeant les données
- Quelques propriétés de la métrique euclidienne
Comme elle est invariable par translation (propriété d'homogénéité) et par rotation (propriété d'isotropie),
d'une projection à l'autre, les distances entre les points restent les mêmes
- tous les points situées à une distance D d'un objet O forment un cercle de centre O et de rayon D
Quand elle est calculée pour des polygones, c'est souvent la distance entre leur centroïde qui est prise en compte.
2.4 La distance rectilinéaire (de Manhattan)
fig. 5 - Distance de Manhattan
Sources : wikipedia
- La position absolue est données par les coordonnées relevées sur la figure 1
formule n°2 - (mem11sig.htm)
tab. 3 - Distances de Manhattan entre les points de la figure 1
DRij 1 2 3 4 5 1 0 30 30 40 170 2 30 0 ? ? ? 3 30 ? 0 ? ? 4 40 ? ? 0 ? 5 170 ? ? ? 0 Il faut compléter le tableau ci-dessus en reprenant le fichier Excel précédent ou en retéléchargeant les données
2.5 Autres distances
- Connaissez-vous d'autres distances ?