Vincent GODARD
Département de Géographie
Université de Paris 8
V.1.3 - Dernière mise à
jour : 03/01/2005
Fiche Mémo n°3.1. du cours de Statistique :
Le mode et la médiane
Les valeurs
centrales ou tendances centrales (mode,
moyenne, médiane, ...)
permettent de
résumer la série brute
1. La médiane
La médiane*:
- est un fractile particulier
c'est donc paramètre de position
- permet de diviser la
distribution en deux sous ensembles égaux
Q2 est la médiane, elle est parfois
notée 
50 % des valeurs lui sont
inférieures
50 % des valeurs lui sont
supérieures
- peut être trouvée :
- graphiquement
Figure 1 : Recherche de la médiane
à l'intersection des courbes de
fréquences cumulées
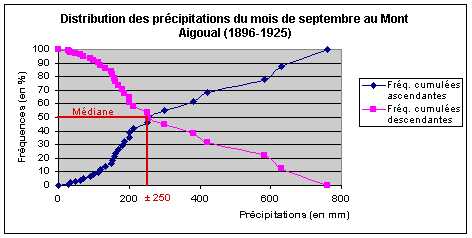
(Sources : Météo France, in SAINT-JULIEN
1999, p.17).
- par le
calcul (cf.
infra)
Contexte :
caractères
quantitatifs et, dans certains cas,
qualitatifs
ordonnables
Objectif :
partitionner la
distribution en 2 classes d'effectifs égaux pour :
- trouver un centre de la
distribution
- comparer le comportement des
50% des plus petits et celui des 50% des plus gros
Réalisation :
- Classer les individus du plus petit au plus
grand
(pose un problème pour classer
les ex-aequo !)
- Diviser la distribution en deux
1.2. Découpage pratique
1.2.1. Dans le cas des données non-groupées
- lorsque N est
impair
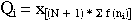 formule
n°1 (mem24sta.htm)
formule
n°1 (mem24sta.htm)
où
Qi est
la médiane ;
X est la valeur de
la médiane ;
i est le
numéro de la médiane ;
N est l'effectif
total ;
ni est l'effectif de la
modalité i pour la médiane ;
f(ni)
est la fréquence de cette modalité ;
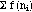 est la fraction (ou fréquence relative
cumulée) de la médiane :
est la fraction (ou fréquence relative
cumulée) de la médiane :
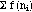 = 1/2 (ou 0,5) si on recherche Q2 le deuxième
quartile.
= 1/2 (ou 0,5) si on recherche Q2 le deuxième
quartile.
- lorsque N est pair
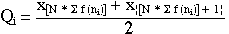 formule
n°2 (mem24sta.htm)
formule
n°2 (mem24sta.htm)
Exemple :
Si l'on prend les températures de Paris,
quelle est la température médiane ?
|
Mois
|
Moy T° à Paris
|
|
janv
|
3,0
|
|
fév
|
3,6
|
|
mars
|
6,6
|
|
avril
|
9,6
|
|
mai
|
13,0
|
|
juin
|
16,0
|
|
juil
|
17,9
|
|
août
|
17,7
|
|
sept
|
15,3
|
|
oct
|
11,2
|
|
nov
|
6,4
|
|
déc
|
3,7
|
Sources :
Météo France
- Ordonner les températures
- Puis effectuer le calcul
Q2 = 10,4
°C
A Paris :
50% des t° moyennes
mensuelles sont inférieures à 10,4 °C
50% des t° moyennes mensuelles sont
supérieures à 10,4 °C
1.2.2. Dans le cas des données groupées
Lorsque l'on n'a pas
accès au tableau élémentaire
Cas fréquent
des statistiques déjà publiées en tableau de
dénombrement
et si l'on ne procède pas par
interpolation, on peut utiliser la formule suivante (cf.
DAGNELIE 1984, vol.1,
p.44) :
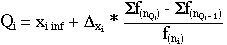 formule
n°3 (mem24sta.htm)
formule
n°3 (mem24sta.htm)
où
Qi est la médiane
;
Xi
inf est la valeur de la borne
inférieure qui contient la médiane ;
i est le
numéro de la médiane ;
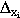 est l'étendue* de la
modalité qui contient la médiane ;
est l'étendue* de la
modalité qui contient la médiane ;
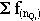 est la fréquence cumulée de la
médiane, exemple :
est la fréquence cumulée de la
médiane, exemple :
- dans le cas des fréquences
cumulées relatives
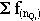 = 0,5 si on recherche Q2 le deuxième quartile
;
= 0,5 si on recherche Q2 le deuxième quartile
;
- dans le cas des fréquences
cumulées absolues
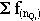 = [(N + 1) * 1/4] si on recherche Q1 le premier quartile pour des
effectifs
impairs ;
= [(N + 1) * 1/4] si on recherche Q1 le premier quartile pour des
effectifs
impairs ;
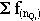 = {[(N/4) + (N/4) + 1] * 1/2} si on recherche
Q1 le
premier quartile pour des effectifs pairs ;
= {[(N/4) + (N/4) + 1] * 1/2} si on recherche
Q1 le
premier quartile pour des effectifs pairs ;
f(ni)
est la fréquence de cette modalité ;
ni est l'effectif de la
modalité i pour le quantile recherché ;
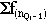 est la fréquence cumulée de la classe
directement inférieure à celle du quantile
recherché.
est la fréquence cumulée de la classe
directement inférieure à celle du quantile
recherché.
- Certains auteurs préconisent
l'utilisation des fréquences absolues, dans la formule,
le résultat serait moins
approximatifs qu'avec les fréquences relatives
Exemple :
|
SAU en ha
|
Nb de fermes
|
|
[0 ; 10[
|
4
|
|
[10 ; 20[
|
10
|
|
[20 ; 30[
|
14
|
|
[30 ; 40[
|
12
|
|
[40 ; 50[
|
10
|
- Quelle est la valeur du 2e quartile
?
Q2 = 28,2 ha
C'est une ferme "théorique", la 25,5e ferme.
1.3. Analyse d'un 1er exemple
Reprendre l'exemple du Tableau 1
(mem24sta.htm) - Distribution des
résidences secondaires dans les villes de plus de 250 000
habitants en France en 1990 - (Sources : RGP, 1990, in
SAINT-JULIEN
1999, p.21).
Téléchargement
du tableau
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
- Prendre le caractère "Nombre de
résidences secondaires pour 1 000 habitants en 1990"
- Quelle est la
valeur de l'agglomération médiane trouvée par
EXCEL ?
Utiliser la fonction médiane
d'EXCEL sur le TIG (tableau élémentaire)
- Peut-on utiliser les
fonctions d'EXCEL sur le tableau de dénombrement 2b
?
- Utiliser les formules vues en cours
(cf. supra) et
comparer les résultats
- Quelle valeur de
médiane vaut-il mieux prendre ?
1.4. Analyse d'un 2e exemple
Reprendre l'exemple du Tableau 2
(mem24sta.htm) - Distribution des
précipitations en Mauritanie entre 1940 et 1990 -
(Sources : ASECNA, ORSTOM).
Téléchargement
du tableau
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
- Calculer la valeur de la médiane pour les
trois stations
- La reporter (manuellement) sur les diagrammes en
boîtes et moustaches
Conclusion :
- La médiane tient compte du
rang de tous les individus et non de leur valeur
- les valeurs exceptionnelles
ne l'affectent pas
- elle est qualifiée d'estimateur robuste
- Valable sur caractères
quantitatifs et qualitatifs ordinaux
- Malgré sa valeur descriptive, elle est
moins utilisée que la moyenne
- Cependant possède une
propriété mathématique qui lui est propre
La médiane est la valeur
centrale la plus proche de tous les individus
 formule
n°1
formule
n°1
Un exemple est développé
dans le CHADULE (CHADULE74, p.50), il permet d'aborder les
problèmes de localisation optimum.
2. Le mode*
Synonyme
: valeur la plus fréquente
- Le mode :
- est la valeur dominante, celle dont la
fréquence est la plus élevée.
- n'est significatif que s'il se détache
franchement
Remarques :
- Il existe des distributions :
- avec un mode principal et un ou
plusieurs modes secondaires
- amodales (sans
mode)
- bi ou plurimodales
Dans le cas de distributions discrétisées (groupées) :
-, la classe
modale* n'est peut-être fonction que
du choix des limites de classes
- le mode est le centre de la classe modale
Reprendre l'exemple du Tableau 1
(mem24sta.htm) - Distribution des
résidences secondaires dans les villes de plus de 250 000
habitants en France en 1990 - (Sources : RGP, 1990, in
SAINT-JULIEN
1999, p.21).
Téléchargement
du tableau
Ce fichier est au format EXCEL 5.0 et "pèse" 97 Ko.
- Prendre le caractère "Nombre de
résidences secondaires pour 1 000 habitants en 1990"
- Quelle est la
valeur modale trouvée par EXCEL ?
- Est-ce la seule ?
- Faire un tableau de dénombrement avec un
pas de 10
- Quelle est la
valeur modale trouvée par EXCEL ?
- Est-ce la seule ?
Conclusion :
- Le mode a une valeur descriptive
importante
- Pour les caractères qualitatifs nominaux c'est la seule
valeur centrale
3. Test de compréhension
|
Communiquez-moi par
courrier
électronique les réponses aux questions
suivantes
Question n°3.1.1.
L'intersection des courbes de fréquences
cumulées croissantes et décroissantes du Mont
Aigoual (Fig. 1) marque la médiane, est-elle :
a) inférieure à 200 mm
b) supérieure à 200 mm
Question n°3.1.2.
Quelle est la station mauritanienne qui a pour
médiane 255,6 mm (Tab. 2, mem24sta.htm) ?
a) Rosso
b) Kaédi
c) Kiffa
Précisez à la rubrique objet
:
EC
statistique
puis dans le
corps du message vos
n°
d'étudiant, nom et prénom
puis vos
réponses
vgodard@univ-paris8.fr
|
Retour au début de la fiche
Mémo
Fiche Mémo suivante
NB : les mots suivis de "*" font
partie du vocabulaire statistique, donc leur définition doit
être connue. Faites-vous un glossaire.
